(This is the first post in a two-part series)
The new “question-of-the-week” is:
What are some best practices for teaching high school mathematics?
As in any subject, there are a zillion different instructional strategies and practices that math teachers can use in high school.
This series will explore recommendations for which might be the best ones.
Today’s contributors are David Wees, Jill Henry, Tammy L. Jones, Leslie A. Texas and Anne Collins. You can listen to a 10-minute conversation I had with David and Jill on my BAM! Radio Show. You can also find a list of, and links to, previous shows here.
I’m not a math teacher, so don’t have much to contribute to this series.
However, you might find this resource collection useful: The Best Apps, Online Tools & Other Resources For Math.
You might also be interested in past math-related posts from this column: Math Instruction
Response From David Wees
David Wees is a formative assessment specialist for New Visions for Public Schools. He has 25 years experience in education and has taught in such far-flung places as NYC, London, Bangkok, and Vancouver. David currently works remotely from his island paradise of Denman Island, British Columbia:
Here are some best practices for teaching high school mathematics that are applicable to a wide variety of pedagogical approaches.
Attend to what your students can do and how they describe what they know consistently and persistently during the year. Keep coming back to prior topics to see if students’ ideas have changed since students’ performance in any single day does not indicate they have learned, learning is the accumulation of long-term change in what students know and can do. Use this information to inform your teaching and to structure feedback opportunities for students. The primary goal of formative assessment is that you and your students are able to use information provided about what they know and can do to increase the likelihood that your students learn the intended content and skills of your course (Wiliam, 2011).
Teach to big ideas rather than 180 disconnected lessons. A big idea takes more than a day to each, and is a deliberate collection of smaller ideas that fit within a lesson. This allows students to have more interconnected schema and requires students to retrieve information from earlier in the year while making connections between topics. We have some examples of big ideas for high school math in our open-source curriculum. Note that it is possible to attend to the details of a calculation that novices find hard to follow, while maintaining a focus on the larger mathematical principles at play.
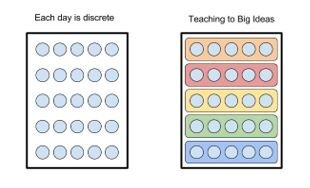
Focus on the processes and connections between different processes rather than just finding the answer. The answer is important, but the processes that lead to answers are far more important to learn. The connections between processes and between different representations of that process are where the core mathematical ideas you want your children to learn reside. This means that while teaching processes, you should use these processes to teach students mathematical principles they can apply to solve problems, not how to solve problem types.
Use instructional routines to support all of your students in having access to the mathematics. Instructional routines shift the cognitive load for students as they focus less on what their role is and what they are supposed to next, since these tasks are delegated to long-term memory, and are therefore more able to focus on learning mathematics (Kelemanik, Lucenta, Creighton, 2016). Instructional routines also support teacher learning by allowing teachers to “keep some parts of their teaching fixed while working on other areas” (Lampert, Graziani, 2009). Another benefit of instructional routines is that they embed retrieval practice opportunities and formative assessment within the routine itself.
When you orchestrate full group discussions, keep a record of the conversation. Trying to follow a conversation where the information contained in the discussion is all new to you is incredibly difficult. Many students will get lost and then disengage from the discussion, leading to less learning.
Be selective and cautious in your use of technology for teaching. Just because a technology is able to demonstrate a mathematical principle for you does not mean your students will have the same experience since you already know the mathematical idea being demonstrated and your students do not. Often I find that students learn how to use a tool to solve mathematical problems but are no more capable at solving problems without using the tool. No mathematical idea when learned should be trapped in the use of a particular technology, since as soon as that technology becomes obsolete or unavailable, students can no longer access the mathematical idea. Note that this does not mean that one should avoid the use of technology, it has incredible potential after all, but that one should pay attention to what students actually learn from using it (just like you should pay attention to what students actually learn from your non-technology based tasks and lessons).
Finally, incorporate what cognitive scientists suggest are high leverage long-term learning strategies. It is possible to treat students as sense-makers while applying these principles from cognitive science to your teaching.
If you have questions about these strategies or any of the linked articles, please let contact @davidwees on Twitter or leave a comment on his blog: http://davidwees.com.

Response From Jillian Henry
Jillian Henry teaches Problem-Based Algebra II and AP Statistics and is the Mathematics Curriculum Coordinator at Flintridge Preparatory School, a 7-12 independent school near Los Angeles. She is an alumnus of the Klingenstein Summer Institute and the Park City Mathematics Institute and received her M.A. in Secondary Mathematics Education from California State University, Northridge:
Embracing Mistakes
A lot of people define themselves by what they’re good at, but don’t ever look to the things they aren’t good at and think, ‘Hey, I can improve on this.’ Error analysis really helps to get into the mindset of learning from mistakes rather than just accepting failure.”
These are the words of one of my 10th grade students, who openly admitted to hating math at the beginning of last school year. Did he love math by June? Maybe not, but engaging in regular error analysis helped him see another side of himself.
We practice informal error analysis daily in my classroom as part of the period’s structure. When students enter each day, they write their work for one of the six to eight homework problems on a white board. For the rest of the period, each student presents his or her work while the other members of class take notes and analyze the problem-solving method being explained. The depth of student-to-student questioning and clarification demonstrates that they are evaluating the work shown rather than just settling for the final answer.
Through this process, students gain confidence in themselves as problem solvers. In an anonymous end-of-year course evaluation, one student described a change in mindset: “In previous years when I saw a math problem that looked daunting, I’d have skipped it. Now I read hard problems a second or third time and try out several ways of solving in an attempt to find a method that works.”
Another student mentioned the value of mistakes for retention: “I thought that [talking about errors] would make me feel bad for not understanding the problem in the first place, but I realized that everyone makes mistakes. For me, figuring out where I went wrong and how to fix it helps me a lot. I often have a better time remembering how to do problem when I made a mistake rather than when I did it right the first time.”
Students also do formal error analysis through test corrections. In fact, we dedicate an entire class period to such self-reflection on the day after a test. Students follow a protocol that involves rewriting their original work and then reworking the problem from scratch. To help with metacognition, students identify the nature of the error - simple, procedural, or conceptual - and devise a plan that will help them avoid that mistake in the future.
My students tend to place a tremendous amount of pressure on themselves when it comes to testing. Demystifying their missteps helps alleviate this pressure and allows them to view assessments as another tool for learning, rather than a device to measure success or failure. “I got it wrong” can turn into “now I know what to do.”
Plenty of students enter my classroom believing they are severely limited in their mathematical abilities. Error analysis can have a profound impact on those students in particular. By normalizing mistakes and providing a safe space for discussion, many students have the same experience that this student recounted: “For me, just having the space to make errors and be able to fix them without judgment or criticism has made learning math easier. I love how we talk over our thought process in class. While I struggle with math, this system keeps me engaged, especially when we are discussing tough problems.”

Response From Tammy L. Jones & Leslie A. Texas
Tammy L. Jones and Leslie A. Texas are co-authors of the 2013 book series from Eye On Education/Routledge-Taylor & Francis Group, Strategies for Common Core Standards for Mathematics: Implementing the Standards for Mathematical Practice (Grades K-5, 6-8, and 9-12) and the 2016 series, Strategic Journeys for Building Logical Reasoning: Activities Across the Content Areas (Grades K-5, 6-8, and 9-12). Collectively, they have 40 years of classroom experience and have also provided professional development in 40 states. Leslie and Tammy model strategies and offer teachers support throughout the school year, a practice that builds capacity at both building and district levels:
One of the biggest challenges facing high school teachers is getting students to want to learn the content required of the course. There are very few students who are excited about mathematics for mathematics sake. In addition, few students believe they are good at math. Therefore, focusing on essential skills that can be used in the math classroom and beyond rather than on mathematical procedures is the key to success. To do this requires employing specific tools and differentiated support.
Students at all levels need to be engaged, challenged, and supported. Here is a beginning list of practices secondary educators can employ to help maximize student success in their classrooms.
Effective educators are:
- providing relevance and context for the mathematics students are learning,
- engaging students using a variety of practices and strategies,
- providing scaffolds for those who need the extra support when working with more challenging content,
- planning intentionally and deliberately so their instruction is impactful, consistent, and effective,
- developing a community of learning where group participation and interaction is expected,
- employing student-centered teaching and student-centered learning,
- providing numerous opportunities for students to develop and strengthen their skills of mathematical communication, including vocabulary, and
- making the development of a variety of problem-solving techniques a priority.
We will focus on the last two as these present unique challenges to secondary educators.
How can we teach students to become independent problem solvers with sound logical reasoning skills?
Here are some simple ideas to begin the process. Let’s start with eliminating the blank piece of paper. It is our belief that most students who disengage, do so because they do not know what to do, not because they don’t care. Therefore, they need strategies for what to do when they don’t know what to do. For example, when assigning a rich task or complex problem, ask students to work independently for a period of time (timed writing) before asking them to partner or before asking for volunteers from the class. This allows all students time to process and make conjectures. Utilize the think-write-pair-share strategy. During the think time, require students to write by doing one of the following: 1) Determine a strategy that could be used to solve the problem; 2) Write a question they have about the problem; 3) Record everything they know about the content related to the problem. This encourages struggling students to take ownership for the work. Before students can partner with others, there must be a response logged.
In our second book series, Strategic Journeys for Building Logical Reasoning: Activities Across the Content Areas, we offer 7 Opportunities for Authentic Writing. A free, downloadable infographic is available that explains these in more detail.
One strategy for helping students become more independent is to develop their ability to ask good questions. Good problem solvers ask good questions about the problems they are attempting to solve. They don’t just jump into doing the math. Typically, there are four opportunities for asking questions while engaged in problem solving: Entry (getting started), Moving (when stuck), Reflection (thinking about thinking), and Extension (deeper thinking). (See White Paper: Opportunities for Questioning Moving Both the Learner and the Learning Forward for more detailed information and a beginning list of questions that can be used.)
If students need assistance while working on a rich task, teachers should provide task-specific questions as feedback to move them forward. Teachers can take the general questions above and modify them to be more task-specific. This models for students how to apply these general questions to any given situation. An infographic, 10 Tips for Effective Questioning is available as a resource for educators.
Research shows how important a role reflection plays for students when learning new material. As a reflection on the logical reasoning process, teachers can have students compare the general questioning tool and the task-specific set of questions to understand how the specific questions were generated. Students can begin to see patterns and understand the idea behind the thought process that occurs during problem-solving/reasoning. This should be done any time there is teacher provided task-specific feedback. Over time, students should begin to internalize the intent of the process.
Students can be asked to use the task-specific questions with their partner as they work. In the beginning, teachers would provide the task-specific feedback questions and ask students to use them as they are supporting each other. The goal is for students to help each other through questioning rather than one student telling another what or how to work. Over time, students can begin to add questions to the list as they generate them in discussion with their partner. The ultimate goal is to have students generate their own task-specific questions. Initially, they may have to use the general questions provided as a guide, but over time, even these would no longer be necessary.
To explicitly facilitate students successfully solving contextual word problems, the following skills would need to be addressed: reading and understanding (decoding) the text; employing a strategy for getting started; having a structure for organizing one’s thinking; and answering the question that was posed rather than responding with the first resulting quantity. To support instruction, we determined there would need to be an explicit of statement of process as well as a graphic organizer to help the student’s employ the process independently. Other tools include a questioning structure, and bridging models that allows students to learn to create questions themselves. (All are explained in more detail in the white paper.)

Response From Anne Collins
Anne Collins is the series editor of NCTM’s publication, Assessment Sampler: Tasks Aligned with Principles and Standards of School Mathematics and Using Classroom Assessment to Improve Student Learning. She is an elected member of the NCTM Board of Directors. Her series of five books titled Zeroing in on Numbers and Operations was published by Stenhouse in 2010:
I think it is very interesting that the question, whether intentionally or not, suggests high school mathematics should be taught differently from elementary or middle school math. The best practices are the same for all levels:
a. pose interesting problems or set a stage for students to pose interesting questions/problems about the situation
b. encourage investigations, experimentations, collaboration and discourse as students explore the problems
c. expect representations or models for the problems being investigated
d. engage students in discourse, creating mathematical arguments and critiquing the reasoning of others,
e. proving their work with both formal and informal proofs.

Thanks to David, Jill, Tammy, Leslie and Anne for their contributions!
Please feel free to leave a comment with your reactions to the topic or directly to anything that has been said in this post.
Consider contributing a question to be answered in a future post. You can send one to me at lferlazzo@epe.org. When you send it in, let me know if I can use your real name if it’s selected or if you’d prefer remaining anonymous and have a pseudonym in mind.
You can also contact me on Twitter at @Larryferlazzo.
Anyone whose question is selected for this weekly column can choose one free book from a number of education publishers.
Education Week has published a collection of posts from this blog, along with new material, in an e-book form. It’s titled Classroom Management Q&As: Expert Strategies for Teaching.
Just a reminder--you can subscribe and receive updates from this blog via email or RSS Reader. And, if you missed any of the highlights from the first six years of this blog, you can see a categorized list below. They don’t include ones from this current year, but you can find them by clicking on the “answers” category found in the sidebar.
This Year’s Most Popular Q&A Posts
Best Ways To Begin The School Year
Best Ways To End The School Year
Student Motivation & Social Emotional Learning
Teaching English Language Learners
Entering The Teaching Profession
I am also creating a Twitter list including all contributers to this column.
Look for Part Two in a few days..
